Calendar Problems
Calendar Problems Shortcut Tricks
Most of the students are having difficulties in solving the Calendar problems. Already many logic are there to solve these kinds of problems, but all these logic are difficult to understand. So here is the simple way to solve calendar problems.

Leap Year: A particular year divisible by 4 is called leap year, also it should not be century year. Example: 1976, 1840 are leap year as they are divisible by 4.
Every Years start and end with same days but in case of leap year, year end with next days.
Each fourth century is a leap year. Example: 400, 800, 1200, 1600, 2000, 2400 are leap years, but 700, 1300, 1900 are not leap years.
Odd Days: For a given number of days, number of days more than complete week are called odd days. Example: in 10 days, there is one week and 3 odd days.
Counting of Weeks and Days in Year
- 1 ordinary year has 365 days = 52 weeks + 1 odd day
- 1 leap year has 366 days = 52 weeks + 2 odd days
- 100 years = 76 ordinary years + 24 leap years = 76*1 + 24*2 = 124 odd days = 17 weeks + 5 odd days
- Since in 100 years, number of odd days are 5
- In 200 years, number of odd days are 5*2= 10 = 1 week + 3 odd days, 3 odd days
- Similarly in 300 years 5*3 = 15 = 2 weeks + 1 odd day
- Similarly for 400 years number of odd days 5*4 + 1 = 0 odd days, from this we conclude that for 800, 1200, 1600 , 2000, 2400 years odd days will be zero
Year Code
| 1600-1699 | >1700-1799 | 1800-1899 | 1900-1999 | 2000-2099 |
| 6 | 4 | 2 | 0 | 6 |
Month Code
| Jan | Feb | Mar | Apr | May | June | July | Aug | Sep | Oct | Nov | Dec |
| 0 | 3 | 3 | 6 | 1 | 4 | 6 | 2 | 5 | 0 | 3 | 5 |
Day Code
| Sun | Mon | Tues | Wed | Thrus | Fri | Sat |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
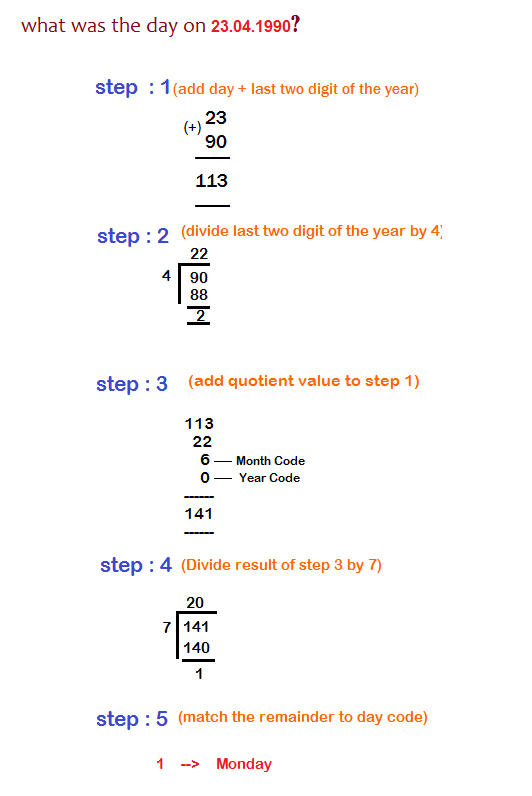
Steps to Solve Calendar Problems
- Add the day digit to last two digit of the year.
- Divide the last two digits of the year by four.
- Add the Quotient value in step 3 to result obtain in step 1.
- Add Month Code and year codes to the result obtain in step 3.
- Divide the result of step 4 by seven.
- Obtain the remainder and match with the day code.
Odd Day Code
| Day | Sun | Mon | Tues | Wed | Thrus | Fri | Sat |
|---|---|---|---|---|---|---|---|
| Odd day no. | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
What was the day of the week on 20 may, 1985 ?
Solution
Here Number of odd days in 1600 years = 0 Number of odd days in 300 years from 1600 to 1900 = 5*3 = 2 week + 1 odd day= 1 odd day Number of odd days in 84 years= 21 leap year + 63 days = 21*2 + 63*1 = 105 days = 0 odd days Number of odd days in 20 may = 31 days of Jan. + 28 days of feb + 31 days of mar + 30 days in april + 20 days in may = 140 days = 0 odd day So total number of odd days = 0+1+0+0=1 = Monday
On what date of Feb. 2007 did Saturday fall ?
Solution
For this find the day of 1.2.2007 1600+400 years has 0 odd days From 2001 to 2006 there are 1 leap years + 5 ordinary years So number of odd days = 1*2 + 5*1 = 2 + 5 = 7 = 1 week = 0 odd day Now from 1.1.2007 to 1.2.2007 number of days = 32 = 4 weeks + 4 odd days = 4 odd days So, total number of odd days = 4, so 1.2.2007 will be Thursday Now Saturday will be on 3.2.2007
Today is Tuesday. After 72 days, it will be ?
Solution
A week has 7 days " Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday ". 72 / 7 = 10 ( Remainder = 2) So you can say that after multiples of 7 days, the day will repeat itself as tuesday. Hence after 70 days Tuesday will occur again. So we calculate after the remainder (2) , the answer is Thursday. Simple Logic = And whatever the remainder obtained is, add that to the day.
Important Points Related to Calendar Problems
- A solar year has 365 days 5 hours 48 minutes and 48 seconds. An ordinary year has 365 days. In order to remove this difference, every fourth year has 366 days and every fourth century is a leap year but no other century is a leap year.
- The number of days more than the complete number of weeks in a given period is the number of odd days for that period.
- In an ordinary year there are 52 weeks and one odd day.
- In a leap year there are 52 weeks and two odd days.
- 100 years contain 5 odd days.
- 200 years contain 3 odd days.
- 300 years contain 1 odd day.
- 400 years contain 0 odd days.
- 1st January 1 A.D. was Monday. So days are counted according to this.: Sunday for 0 odd days: Monday for 1 odd day; Tuesday for 2 odd days, and so on.
Same Answer For Following Questions :
- If today is Tuesday, then what will be the day after 72 days? = Thursday
- If today is Tuesday, what day of the week would it be 72 days from now? = Thursday
- If today is Tuesday, then what will be the day after 72 days? = Thursday
- If today is Tuesday, after 72 days, which day of the week will it be? = Thursday
- If today is Tuesday, then which day will it be in 72 days? = Thursday
- If today is Tuesday, what day is it 72 days from now? = Thursday
- If today is Tuesday, then which day will it be in 72 days? = Thursday
- Today is Tuesday. What day of the week will it be in 72 days time? = Thursday
- If today is Tuesday, on what day will you meet your friend after 72 days? = Thursday
- If today is Tuesday, then what day will come after 72 days from today? = Thursday

