Number System Problems
Number System Aptitude
Number system is one of the fundamental topics in the quantitative aptitude section of any Exam.
In Decimal number system, there are ten symbols namely 0,1,2,3,4,5,6,7,8 and 9 called digits. A number is denoted by group of these digits called as numerals.
Face value of a digit in a numeral is value of the digit itself. For example in 321, face value of 1 is 1, face value of 2 is 2 and face value of 3 is 3.
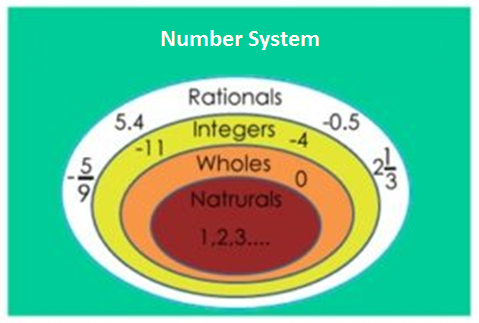
Types Of Number
Natural Number: Natural Numbers - n > 0 where n is counting number; [1,2,3...]. Numbers used in counting are termed as natural numbers. Example N={ 1, 2, 3, 4, 5, ....}
Whole Number: Whole Numbers - n ≥ 0 where n is counting number; [0,1,2,3...]. Natural numbers with 0 are termed as whole number. Example W={0, 1, 2, 3, 4, ......}
Prime number: A number which is not divisible by other numbers except the number itself and 1 is termed as prime number. Example 19 is a prime number because it is not divisible by other than 1 and 19
Composite Numbers: Numbers other than one which are not prime are termed as Composite numbers. Example 4, 6, 8, 9, 12
Even Numbers: Numbers which are divisible by 2 ae termed as even numbers. Example 2, 4, 6, 8, 10
Odd Numbers: The number which is not divisible by 2 are termed as odd numbers. Example 3, 7, 9, 11
Consecutive numbers: Numbers increasing by one are termed as consecutive numbers. Example 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13
Integers: The set of numbers which consists of Negative numbers and whole numbers is known as Integers. ExampleI= { ....-5, -4, -3, -2, -1, 0, 1, 2, 3, 4..... }
Rational Numbers: The numbers which can be written in the form P / Q , where P and Q are integers and Q not equal to zero is termed as Rational Numbers. Example (1/2), (3/7), (7/11)
Irrational Numbers: The numbers which can not be written in P / Q form are termed as Irrational Numbers 22
Real Numbers: Real number consists of both rational as well as irrational numbers.
Negative Integers: The numbers -1, -2, -3, ... are called negative integers.
Positive Fractions: The numbers(2/3) ,(4/5) ,(7/8) ... are called positive fractions.
Negative Fractions: The numbers -(6/8) ,-(7/19) , -(12/17) ... are called negative fractions.
Note: 0 is the only whole number which is not a natural number. Every natural number is a whole number.
Prime Numbers: Numbers which is divisible by themselves only apart from 1.
Composite Numbers: Non-prime numbers > 1. For example, 4,6,8,9 etc. 1 is neither a prime number nor a composite number. 2 is the only even prime number.
Co-Primes Numbers: Two natural numbers are co-primes if their H.C.F. is 1. For example, (2,3), (4,5) are co-primes.
Rational Numbers: Any number which is a positive or negative integer or fraction, or zero is called a rational number. A rational number is one which can be expressed in the following format (a/b) , where b ≠ 0 and a & b are positive or negative integers. Irrational Numbers: An infinite non-recurring decimal number is known as an irrational number. These numbers cannot be expressed in the form of a proper fraction a/b where b ≠ 0. e.g.√2 , √5 , Π, etc.
Even Numbers: The integers which are divisible by 2 are called even numbers e.g. -4, 0, 2, 16 etc.
Odd Numbers: The integers which are not divisible by 2 are odd numbers e.g. -7, -15, 5, 9 etc.
Prime Numbers: Those numbers, which are divisible only by themselves and 1, are called prime numbers. In other words, a number, which has only two factors, 1 and itself, is called a prime number. e.g. 2, 3, 5, 7, etc.
Note: 2 is the only even prime number.
Composite Number: A number, which has factors other than itself and 1, is called a composite number. e.g. 9, 16, 25...
Note: 1 is neither a composite number nor a prime number.
Real Numbers: The natural numbers, integers, whole numbers, rational numbers and irrational numbers constitute the set of real numbers. Every real number can be represented by a point on a number line.
Divisible Properties
- Divisibility by 2 - A number is divisible by 2 if its unit digit is 0,2,4,6 or 8.
- Divisibility by 3 - A number is divisible by 3 if sum of its digits is completely divisible by 3.
- Divisibility by 4 - A number is divisible by 4 if number formed using its last two digits is completely divisible by 4.
- Divisibility by 5 - A number is divisible by 5 if its unit digit is 0 or 5.
- Divisibility by 6 - A number is divisible by 6 if the number is divisible by both 2 and 3.
- Divisibility by 8 - A number is divisible by 8 if number formed using its last three digits is completely divisible by 8.
- Divisibility by 9 - A number is divisible by 9 if sum of its digits is completely divisible by 9.
- Divisibility by 10 - A number is divisible by 10 if its unit digit is 0.
- Divisibility by 11 - A number is divisible by 11 if difference between sum of digits at odd places and sum of digits at even places is either 0 or is divisible by 11.
Tips on Division
- If a number n is divisible by two co-primes numbers a, b then n is divisible by ab.
- (a-b) always divides (an - bn) if n is a natural number.
- (a+b) always divides (an - bn) if n is an even number.
- (a+b) always divides (an + bn) if n is an odd number.

