Height and Distance Problems

Aptitude Height and Distance Problems

One of the important applications of trigonometry is in finding the height and distances of the point which are not directly measurable. This is done with the help of trigonometric ratios. To solve any height and distance problem first do these things;

• Step 1: Draw a sketch of the situation given.
• Step 2: Mark in the given angle of elevation or depression and other information.
• Step 3: Use trigonometry to find the required missing length

Trigonometry

Angle of Elevation

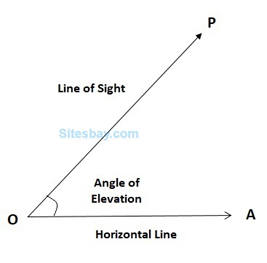
Suppose a man from a point O looks up at an object P, placed above the level of his eye. Then, the angle which the line of sight makes with the horizontal through O, is called the angle of elevation of P as seen from O.

Angle of elevation of P from O = △AOP.

Angle of Depression

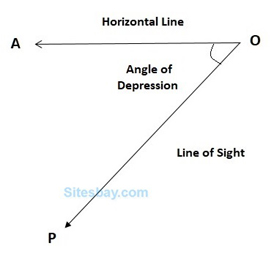
Suppose a man from a point O looks down at an object P, placed below the level of his eye, then the angle which the line of sight makes with the horizontal through O, is called the angle of depression of P as seen from O.

Values Trigonometric Ratios

Find the distance/height/base/length when angle is given

Question: A boy is flying a kite in the evening. The thread of the kite was 120 m long and the angle of elevation with the boy's eyes was 30°. Find the height of the kite?

tips and tricks and shortcuts for height and distance

Sin 30° = Perpendicular/Hypotenuse = AB/AC
1/2 = h/120
h = 60 m

Find the angle when distance/height/base/length is given

Question: Find the angle of elevation of the sun when the shadow of a pole of 18 m height is 6√3 m long?

tips and tricks and shortcuts for height and distance

Let AB be the pole and CB be the shadow
Given that AB = 18 m and CB = 6√3
Let the angle of elevation, ACB = θ
From the right triange ABC,
Tan θ = Perpendicular/Base = AB/BC = 18/6√3 = 3/√3 = √3
Therefore,
θ =tan–1(√3)=60°