Problems on HCF

Problems on HCF Shortcut Tricks

Common Multiple: Defined as number which is exactly divisible by each of the numbers under consideration. Example 4 is a common factor of 8, 12, 16, 20, 24

Highest Common Multiple(HCF): HCF of two or more numbers is the greatest number that divides each of them exactly.

Method of Prime Factors

Break the given numbers into prime factors and find the product of common prime factors, product will be HCF.

Find the HCF of 42 and 70

42=2*3*7,   70=2*5*7 So HCF will be 2*7 =14
Find the HCF of 24, 45, 60
Solution-  24 = 2*2*2*3  45= 3*3*5  60= 2*2*3*5   
So HCF of 24, 45 and 60 is 3

Find HCF of 12 and 15

The factors of 12 are : 1, 2, 3, 4, 6, 12.
The factors of 15 are : 1, 3, 5, 15.
1 and 3 are the only common factors (numbers which are factors of both 12 and 15).
Therefore, the highest common factor of 12 and 15 is 3.

Finding HCF with prime factorisations

We want to find the HCF of the numbers 60 and 72.
Start by writing each number as a product of its prime factors.
60 = 2 * 2 * 3 * 5
72 = 2 * 2 * 2 * 3 * 3

To make the next stage easier, we need to write these so that each new prime factor begins in the same place:

60	= 2	* 2		* 3		* 5
72	= 2	* 2	* 2	* 3	* 3	

All the "2"s are now above each other, as are the "3"s etc. This allows us to match up the prime factors.
The lowest common multiple is found by multiplying all the factors which appear in either list:

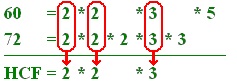
So the HCF of 60 and 72 is 2 × 2 × 3 which is 12.